Introduction
In a previous Math Scholar blog, we presented Archimedes’ ingenious scheme for approximating $\pi$, based on an analysis of regular circumscribed and inscribed polygons with $3 \cdot 2^k$ sides, using modern mathematical notation and techniques.
One motivation for both the previous blog and this blog is to respond to some recent writers who reject basic mathematical theory and the accepted value of $\pi$, claiming instead that they have found $\pi$ to be a different value. For example, one author asserts that $\pi = 17 – 8 \sqrt{3} = 3.1435935394\ldots$. Another author asserts that $\pi = (14 – \sqrt{2}) / 4 = 3.1464466094\ldots$. A third author promises to reveal an “exact” value of $\pi$, differing significantly from the accepted value. For other examples, see this Math Scholar blog. Of course, $\pi$ cannot possibly be given by any algebraic expression such as these, since $\pi$ was proven transcendental by Lindemann in 1882, and his proof has been checked carefully by many thousands of mathematicians since then.
To that end, the previous blog presented a rigorous proof of Archimedes’ method, demonstrating that $\pi = 3.1415926535\ldots$ and certainly not any variant values. It employed only basic algebra, trigonometry and the Pythagorean theorem, and avoided calculus, analysis or any reasoning that depends on properties of $\pi$.
N-sided polygons
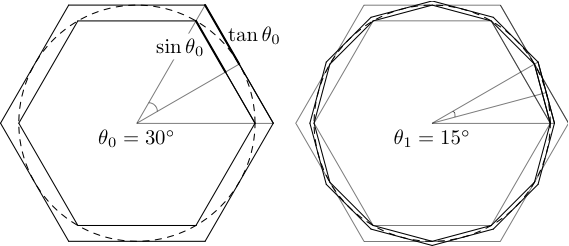
As mentioned above, Archimedes’ construction was based on polygons with $3 \cdot 2^k$ sides, and the presentation of this scheme in the previous blog followed this convention.
However, strictly speaking from a modern perspective, $\pi$ is most commonly defined as the circumference of a circle divided by its diameter (or as the semi-circumference of a circle of radius one), where the circumference of a circle is defined as the limit of the perimeters of circumscribed or inscribed regular polygons with $n$ sides, as $n$ increases without bound. Note that this is a somewhat stricter definition than Archimedean definition, which only deals with the special case $n = 3 \cdot 2^k$, leaving open the question of other $n$.
In the spirit of adhering to the modern convention, we present here a complete proof that $\pi$ as defined by Archimedes is the same as $\pi$ based on general $n$-sided regular polygons. As a bonus, we also present a proof that the limits of the areas of these polygons is also equal to $\pi$. These proofs are a bit more difficult than with the Archimedean case $n = 3 \cdot 2^k$ (see the previous blog), but still can be presented entirely using only basic algebra and trigonometry, with no need to resort to calculus, complex numbers or any other topic not familiar to a standard high-school mathematics curriculum. As with the previous blog, traditional degree notation is used here for angles instead of the radian measure customary in professional research work, both to make the presentation easier follow and also to avoid any concepts or techniques that might be viewed as dependent on $\pi$.
We start by establishing some well-known trigonometric identities. Readers who are familiar with these identities may skip to the next section.
LEMMA 1 (Sine, cosine and tangent of a sum):
$$\sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta),$$ $$\cos(\alpha + \beta) = \cos(\alpha) \cos(\beta) – \sin(\alpha) \sin(\beta),$$ $$\tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 – \tan(\alpha)\tan(\beta)}.$$ Proof: These identities were proved in the previous article, relying only on simple geometry and the Pythagorean theorem. See also this Wikipedia article.
LEMMA 2 (Multi-angle inequalities):
Let $\alpha$ be any angle and $n \ge 2$ be any positive integer such that $0 \lt n \alpha \lt 45^\circ$. Then $\sin(n \alpha) \lt n \sin(\alpha)$ and $\tan(n \alpha) \gt n \tan(\alpha).$
Proof: These identities can be proved most easily using an induction argument: Clearly they hold for $n = 2$, since $\sin(2 \alpha) = 2 \sin(\alpha) \cos(\alpha) \lt 2 \sin\alpha$, and $\tan (2 \alpha) = 2 \tan (\alpha) / (1 – \tan^2(\alpha)) > 2 \tan(\alpha)$. Then assuming the inequalities hold for $n$, note that $$\sin((n+1) \alpha) = \sin(n \alpha) \cos(\alpha) + \cos(n \alpha) \sin(\alpha) \lt n \sin(\alpha) + \sin(\alpha) = (n+1) \sin(\alpha),$$ $$\tan((n+1) \alpha) = (\tan(n \alpha) + \tan(\alpha)) / (1 – \tan(n \alpha) \tan(\alpha)) \gt n \tan(\alpha) + \tan(\alpha) = (n + 1) \tan(\alpha),$$ so that the inequalities hold for $n+1$ also.
LEMMA 3 (Ratios of multi-angle sines and tangents).
Let $\alpha$ be any angle and $n \ge 2$ be any positive integer such that $0 \lt n \alpha \lt 45^\circ$. Then $$\frac{\sin((n+1) \alpha)}{\sin(n \alpha)} \lt \frac{n+1}{n,}$$ $$\frac{\tan((n+1) \alpha)}{\tan(n \alpha)} \gt \frac{n+1}{n}.$$ Proof: First note that for $0 \lt n \alpha \lt 45^\circ$, $\sqrt{3}/2 \lt \cos(\alpha) \lt 1$ and $0 \lt \tan(\alpha) \lt 1$ (and also for $n \alpha$ in place of $\alpha$). Then we can write $$\frac{\sin((n+1) \alpha)}{\sin(n \alpha)} = \frac{\sin(n \alpha) \cos (\alpha) + \cos(n \alpha) \sin(\alpha)}{\sin(n \alpha)} = \cos (\alpha)\left(1 + \frac{\tan(\alpha)}{\tan(n \alpha)}\right) \lt 1 + \frac{\tan(\alpha)}{\tan(n \alpha)} \lt 1 + \frac{1}{n},$$ where we applied Lemma 2 at the final step. The second requires a bit more work: $$\frac{\tan((n+1)\alpha)}{\tan(n\alpha)} = \frac{\tan(n \alpha) + \tan(\alpha)}{\tan(n \alpha) (1 – \tan (n \alpha) \tan(\alpha))} = \frac{1 + \tan{\alpha}/\tan(n \alpha)}{1 – \tan(n \alpha) \tan(\alpha)} = \left(1 + \frac{\tan(\alpha)}{\tan(n \alpha)}\right) \cdot \left(1 + \frac{\tan(n \alpha) \tan(\alpha)}{1 – \tan(n \alpha) \tan(\alpha)}\right) $$ $$\gt \left(1 + \frac{\tan(\alpha)}{\tan(n \alpha)}\right) \cdot \left(1 + \tan(n \alpha) \tan(\alpha)\right) = 1 + \frac{\tan(\alpha)}{\tan(n \alpha)} + \tan(n \alpha) \tan(\alpha) + \tan^2(\alpha)$$ $$\gt 1 + \frac{\tan(\alpha)}{\tan(n \alpha)} \left(1 + \tan^2(n \alpha)\right) = 1 + \frac{\tan(\alpha)}{\tan(n \alpha) \cos^2(n \alpha)} = 1 + \frac{\sin(\alpha)}{\sin(n \alpha) \cos(n \alpha) \cos(\alpha)} > 1 + \frac{\sin(\alpha)}{\sin(n \alpha)} \gt 1 + \frac{1}{n},$$ where again we employed Lemma 2 at the final step.
AXIOM 1 (Completeness axiom): Every set of reals that is bounded above has a least upper bound; every set of reals that is bounded below has a greatest lower bound.
Comment: This fundamental axiom of real numbers merely states the property that the set of real numbers, unlike say the set of rational numbers, has no “holes.” An equivalent statement of the completeness axiom is “Every Cauchy sequence of real numbers has a limit in the real numbers.” See the Wikipedia article Completeness of the real numbers and this Chapter for details.
THEOREM 1 (Pi as the limit of n-sided circumscribed and inscribed regular polygons):
Theorem 1a: For a circle of radius one, as the index $n \ge 6$ increases, the greatest lower bound of the semi-perimeters of circumscribed regular polygons with $n$ sides is exactly equal to the least upper bound of the semi-perimeters of inscribed regular polygons with $n$ sides, which value is exactly the same as $\pi$ as defined by Archimedes as in the previous blog.
Theorem 1b: For a circle of radius one, as the index $n \ge 6$ increases, the greatest lower bound of the areas of circumscribed regular polygons with $n$ sides is exactly equal to the least upper bound of the areas of inscribed regular polygons with $n$ sides, which value is exactly equal to $\pi$ as defined in Theorem 1a and in the previous blog.
Proof strategy: We will show that (a) the sequence of circumscribed semi-perimeters $(p_n)$ is strictly decreasing; (b) the sequence of inscribed semi-perimeters $(q_n)$ is strictly increasing; (c) all $(p_n)$ are strictly greater than all $(q_n)$; and (d) the distance between $p_n$ and $q_n$ becomes arbitrarily small for large $n$. Thus the greatest lower bound of the circumscribed semi-perimeters is equal to the least upper bound of inscribed semi-perimeters, and this common limit coincides with $\pi$ as defined by Archimedes in terms of polygons with $3 \cdot 2^k$ sides. A similar argument reaches the same conclusion for the sequence of circumscribed and inscribed areas.
Proof: For the entirety of this proof, we will assume $n \ge 6$. Let $p_n$ be the semi-perimeter of an $n$-sided regular circumscribed polygon for a circle with radius one, and let $q_n$ be the semi-perimeter for an $n$-sided regular inscribed polygon for a circle with radius one. By examining the figure (see also the previous blog), it is clear that $p_n = n \tan (180^\circ/n)$ and $q_n = n \sin (180^\circ/n)$. Note, for instance, that $p_6 = 6 \tan (30^\circ) = 2 \sqrt{3} = 3.46419\ldots$ and $q_6 = 6 \sin(60^\circ) = 3$. Now let $\alpha = 180^\circ/ (n(n+1))$. By applying Lemma 3, we can then write $$\frac{p_{n+1}}{p_n} = \frac{(n+1) \tan(180^\circ/(n+1))}{n \tan (180^\circ/n)} = \frac{(n+1) \tan (n \alpha)}{n \tan((n+1) \alpha)} \lt 1,$$ $$\frac{q_{n+1}}{q_n} = \frac{(n+1) \sin(180^\circ/(n+1))}{n \sin (180^\circ/n)} = \frac{(n+1) \sin(n \alpha)}{n \sin ((n+1) \alpha)} \gt 1,$$ so that $(p_n)$ is a strictly decreasing sequence and $(q_n)$ is a strictly increasing sequence. Let $\beta = 180^\circ / n$. For $n \ge 6$ note that $1/2 \lt \sqrt{3}/3 \lt \cos(\beta) \lt 1$. Then we can write $$p_n – q_n = n \tan(\beta) – n \sin(\beta) = \frac{n \sin(\beta)}{\cos(\beta)} \left(1 – \cos(\beta)\right) \gt 0,$$ so that each $p_n \gt q_n$. If $n \gt m$, then $p_n \gt q_n \gt q_m$, so $p_n \gt q_m$. Thus all $p_n$ are strictly greater than all $q_n$. In particular, since $p_6 = 2 \sqrt{3} \lt 4$, this means that all $p_n \lt 4$ and thus all $q_n \lt 4$. Similarly, since $q_6 = 3$, all $q_n \ge 3$ and thus all $p_n \gt 3$. By continuing with the last-written equality above, $$p_n – q_n = \frac{n \sin(\beta)}{\cos(\beta)} \left(1 – \cos(\beta)\right) = \frac{n \sin(\beta) (1 – \cos^2 (\beta)}{\cos(\beta)(1 + \cos(\beta))} = \frac{n \sin^3(\beta)}{\cos(\beta) (1 + \cos(\beta))} \lt 2 n \sin^3(\beta) = \frac{2 q_n^3}{n^2} \lt \frac{128}{n^2},$$ since $\cos(\beta) \gt 1/2$ and all $q_n \lt 4$. Thus the difference between $p_n$ and $q_n$ decreases to arbitrarily small values for large $n$.
Recall from the above that all $p_n \gt 3$, so that the sequence $(p_n)$ of circumscribed semi-perimeters is bounded below. Thus by Axiom 1 the sequence $(p_n)$ has a greatest lower bound $L_1$. In fact, since all $p_n$ are greater than all $q_n$, any $q_n$ is a lower bound of the entire sequence $(p_n)$, so that we may write, for any $n \ge 6$, $p_n \geq L_1 \geq q_n$. Also, all $q_n \lt 4$, so that the sequence $(q_n)$ of inscribed semi-perimeters is bounded above, and thus has a least upper bound $L_2$. And, as before, since any $p_n$ is an upper bound for the entire sequence $(q_n)$, it also follows that $p_n \geq L_2 \geq q_n$. Thus both $L_1$ and $L_2$ are “squeezed” between $p_n$ and $q_n$, which, for sufficiently large $n$, are arbitrarily close to each other (according to the last displayed equation above), so that $L_1$ must equal $L_2$. Since the sequences $(p_n)$ and $(q_n)$ include the special case $n = 3 \cdot 2^k$, and the limits for these special cases have the common value $\pi$, this means that the common limits for the full sequences $(p_n)$ and $(q_n)$ are also equal to $\pi$. This completes the proof of Theorem 1a.
For Theorem 1b, let $r_n$ and $s_n$ denote the areas of the circumscribed and inscribed regular polygons for a circle of radius one. By examining the figure above (see also the previous blog), it can be seen that $r_n = n \tan (180^\circ/n)$ and $s_n = n \sin (180^\circ/n) \cos(180^\circ/n)$. Let $\beta = 180^\circ/n$. Now note that the difference between the circumscribed and inscribed areas is $$r_n – s_n = n (\tan(\beta_n) – \sin(\beta)\cos(\beta)) = n \left(\frac{\sin(\beta}{\cos(\beta)} – \sin(\beta) \cos(\beta)\right) $$ $$= \frac{n \sin(\beta) (1 – \cos^2(\beta))}{\cos(\beta)} = \frac{n \sin^3(\beta)}{\cos(\beta)} \lt 2n \sin^3(\beta) \lt \frac{128}{n^2},$$ since the final inequality was established a few lines above. As before, it follows that the greatest lower bound of the circumscribed areas $r_n$ is exactly equal to the least upper bound of the inscribed areas $s_n$. Furthermore, since the sequence $(p_n)$ of semi-perimeters of the circumscribed polygons is exactly the same sequence as the sequence $(r_n)$ of areas of the circumscribed polygons, we conclude that the common limit of the areas is identical to the common limit of the semi-perimeters, namely $\pi$. This completes the proof of Theorem 1b.
Other formulas and algorithms for Pi
We note in conclusion that Archimedes’ scheme is just one of the many known formulas and algorithms for $\pi$. See for example this collection. One such formula is the Borwein quartic algorithm: Set $a_0 = 6 – 4\sqrt{2}$ and $y_0 = \sqrt{2} – 1$. Iterate, for $k \ge 0$, $$y_{k+1} = \frac{1 – (1 – y_k^4)^{1/4}}{1 + (1 – y_k^4)^{1/4}},$$ $$a_{k+1} = a_k (1 + y_{k+1})^4 – 2^{2k+3} (1 + y_{k+1} + y_{k+1}^2).$$ Then $1/a_k$ converges quartically to $\pi$: each iteration approximately quadruples the number of correct digits. Just three iterations yield 171 correct digits, which are as follows: $$3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482$$ $$534211706798214808651328230664709384460955058223172535940812848111745028410270193\ldots$$
Other posts in the “Simple proofs” series
The other posts in the “Simple proofs of great theorems” series are available Here.