Bach as “mathematician”
Johan Sebastian Bach (1685-1750) regularly garners the top spot in listings of the greatest Western classical composers, typically followed by Mozart and Beethoven. Certainly in terms of sheer volume of compositions, Bach reigns supreme. The Bach-Werke-Verzeichnis (BWV) catalogue lists 1128 compositions, from short solo pieces to the magnificent Mass in B Minor (BWV 232) and Christmas Oratorio (BWV 248), far more than any other classical composer. Further, Bach’s clever, syncopated style led the way to twentieth century musical innovations, notably jazz.
There does seem to be a credible connection between the sort of mental gymnastics done by a mathematician and by a musician. To begin with, there are well-known mathematical relationships between the pitch of various notes on the musical keyboard. But beyond mere analysis of pitches, it is clear that the arena of musical syntax and structure has a very deep connection to the sorts of syntax, structure and other regularities that are studied in mathematical research. Bach and Mozart in particular are well-known for music that is both “mathematically” beautiful and structurally impeccable.

Albert Einstein playing his violin
For additional details on Bach’s “mathematical” style, some interesting speculations on golden ratio patterns in Bach’s music, as well as a listing of number of particularly listenable works, with audio links, see this previously published Math Scholar article: Bach as mathematician.
Using network theory to analyze Bach’s music
In February 2024, a team of researchers from the University of Pennsylvania, Yale and Princeton in the U.S. published a study describing their efforts to analyze Bach’s music using network theory and information theory. As the authors explain,
Bach is a natural case study given his prolific career, the wide appreciation his compositions have garnered, and the influence he had over contemporaneous and subsequent composers. His diverse compositions (from chorales to fugues) for a wide range of musicians (from singers to orchestra members) often share a fundamental underlying structure of repeated—and almost mathematical—musical themes and motifs. These features of Bach’s compositions make them particularly interesting to study using a mathematical framework.
The authors included a wide range of Bach compositions in their study, including some preludes and fugues from the Well-Tempered Clavier suite, two- and three-part inventions, a selection of Bach’s cantatas, the English suites, the French suites, some chorales, the Brandenburg concertos, and various toccatas and concertos.
Overall, their results have confirmed that Bach’s works have a high information content, and further that different subsets of works have distinct characteristics.
Methodology
Here is an outline of their methodology: After collecting digitized versions of the above musical selections, they represented each note as a node in a network, with notes from different octaves as distinct nodes. A transition from note A to note B is represented as a directed edge from A to B. Chords are represented with edges between all notes in the first chord to all notes in the second chord. A graphical representation of this process is shown below. To the right of this illustration is the result of this process for four specific Bach compositions: (a) the chorale “Wir glauben all an einen Gott” (BWV 437); (b) Fugue 11 from the Well-Tempered Clavier (WTC), Book I (BWV 856); (c) Prelude 9 from the WTC, Book II (BWV 878); and (d) Toccata in G major for harpsichord (BWV 916).
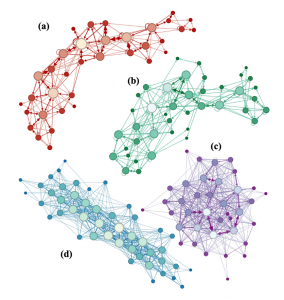
Four examples of note transition networks from Bach’s works: (a) a chorale (BWV 437); (b) Fugue 11 from the WTC, Book I (BWV 856); (c) Prelude 9 from the WTC, Book II (BWV 878); and (d) Toccata in G major (BWV 916); credit: see link to article in main text
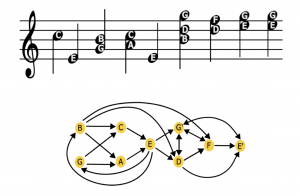
Example of network constructed from a simple musical score; credit: see link to article in main text
The information exhibited in these graphs was quantified as the Shannon entropy of a random walk on the network. In particular, the contribution of the $i$-th node to the entropy is:
$$S_i \; = \; – \sum_{j=1}^n P_{i,j} \log P_{i,j},$$
where $P_{i,j}$ is the transition probability of going from node $i$ to node $j$. Then the entropy of the entire network is a weighted sum of the $S_i$:
$$S \; = \; \sum_{i=1}^m w_i S_i \; = \; – \sum_{i=1}^m w_i \sum_{j=1}^n P_{i,j} \log P_{i,j},$$
where the weights $w_i$ are the stationary distribution probabilities: $w_i$ is the probability that a walker ends up at node $i$ after infinite time.
Some additional information and complete technical details are in the published paper.
Results
The researchers found that, indeed, compared with some other musical compositions they had studied, the Bach pieces tended to have higher information content. What was even more interesting was that the researchers found significant differences between the different classes of Bach compositions:
The chorales, typically meant to be sung by groups in ecclesiastical settings, are shorter and simpler diatonic pieces that display a markedly lower entropy than the rest of the compositions studied. By contrast, the toccatas, characterized by more complex chromatic sections that span a wider melodic range, have a much higher entropy. It is possible that the chorales’ functions of meditation, adoration, and supplication are best supported by predictability and hence low entropy, whereas the entertainment functions of the toccatas and preludes are best supported by unpredictability and hence high entropy.
Full details of the results are given in the published paper.
Future directions
The researchers have clearly identified a very interesting and very effective technique to analyze, classify and compare musical compositions. Numerous questions for future research could be asked, some of which were suggested by the authors themselves in their concluding section. Here are a few of these potential research questions, including some due to the present author:
- The authors found that Bach’s music networks had a higher number of transitive triangular clusters, enabling them to be learned more efficiently than arbitrary transition structures. Are pieces with a larger number of these triangles also more appealing to a listener?
- How effective are these techniques in analyzing other classical composers?
- How has the information content of a specific composer changed over time?
- Within a single genre such as classical music, how has the information content of the music changed over time?
- How effective are these techniques in analyzing other genres of music, such as modern jazz, hip-hop and country?
- How do these results compare for various non-Western music genres, such traditional Japanese music (ongaku), Cantonese opera, African tribal music, Tibetan throat singing and Scottish piobaireachd?
- How do human perceptions of music correlate with these measures?
- Do these results offer any insights into the human psychology of musical experience, such as the fundamental question of why humans have evolved to perform and value music?
Clearly an exciting future lies ahead in the realm of fusing mathematical network and information theory with the fine arts.
