Updated 1 February 2024

Space aliens made this rock
Extraterrestrial aliens made this rock
While out hiking, I found this rock. The following table gives measurements made on the rock. The first two rows give the overall length and width of the rock. Each of the next six rows, after the first two, gives thickness measurements, made on a 3cm x 6cm grid of points from the top surface. All measurements are in millimeters:
| Measurement or row | Column 1 | Column 2 | Column 3 |
| Length | 105.0 | ||
| Width | 48.21 | ||
| Row 1 | 35.44 | 35.38 | 36.54 |
| Row 2 | 38.06 | 38.27 | 38.55 |
| Row 3 | 38.02 | 39.53 | 39.29 |
| Row 4 | 38.66 | 40.50 | 41.96 |
| Row 5 | 39.40 | 43.48 | 43.31 |
| Row 6 | 39.58 | 41.83 | 43.07 |
This is a set of 20 measurements, each given to four significant figures, for a total of 80 digits. Among all rocks of roughly this size, the probability of a rock appearing with this particular set of measurements is thus one in 1080. Note that this probability is so remote that even if the surfaces of each of the ten planets estimated to orbit each of 100 billion stars in the Milky Way were examined in detail, and this were repeated for each of the estimated 100 billion galaxies in the visible universe, it is still exceedingly unlikely that a rock with this exact set of measurements would ever be found. Thus this rock could not have appeared naturally, and must have been created by space aliens…
Wait a minute! It is just an ordinary rock!
What is the fallacy in the above argument? First of all, modeling each measurement as a random variable of four equiprobable digits, and then assuming all measurements are independent (so that we can blithely multiply probabilities) is a very dubious reckoning. In real rocks, the measurement at one point is constrained by physics and geology to be reasonably close to that of nearby points. Presuming that every instance in the space of 1080 theoretical digit strings is equally probable as a set of rock measurements is an unjustified and clearly invalid assumption. Thus the above reckoning must be rejected on this basis alone.
The post-hoc probability fallacy

A 13-card hand dealt “at random”
Key point: It is important to note that the post-hoc fallacy does not just weaken a probability or statistical argument. In most cases, the post-hoc fallacy completely nullifies the argument. The correct reckoning is “What is the probability of X occurring, given that X has been observed to occur,” which of course is unity. In other words, the laws of probability, when correctly applied to a post-hoc phenomenon, can say nothing one way or the other about the likelihood of the event.
In general, probability reckonings based solely or largely on combinatorial enumerations of theoretical possibilities have no credibility when applied to real-world problems. And reckonings where a statistical test or probability calculation is devised or modified after the fact are invalid and should be immediately rejected — some outcome had to occur, and the laws of probability by themselves cannot help to determine its likelihood.
The post-hoc fallacy in biology
One example of the post hoc probability fallacy in biology can be seen in the attempt by some evolution skeptics (see this Math Scholar article for some references) to claim that the human alpha-globin molecule, a component of hemoglobin that performs a key oxygen transfer function in blood, could not have arisen by “random” evolution. These writers argue that since human alpha-globin is a protein chain based on a sequence of 141 amino acids, and since there are 20 different amino acids common in living systems, the “probability” of selecting human alpha-globin at random is one in 20141, or one in approximately 10183. This probability is so tiny, so they argue, that even after millions of years of random molecular trials covering the entire Earth’s surface, no human alpha-globin protein molecule would ever appear.
But this line of reasoning is a dead-ringer for the post-hoc probability fallacy. Note that this probability reckoning was performed after the fact, on a single very limited dataset (the human alpha-globin sequence) that has been known in the biology literature for decades. Some sequence had to appear, and the fact that the particular sequence found today in humans was the end result of the course of evolution provides no guidance, by itself, as to the probability of its occurrence.
Further, just like the rock measurements above, the enumeration of combinatorial possibilities in this calculation, devoid of empirical data, has no credibility. Some alpha-globin sequences may be highly likely to be realized while others may be biologically impossible. It may well be that there is nothing special whatsoever about the human alpha-globin sequence, as evidenced, for example, by the great variety in alpha-globin molecules seen across the biological kingdom, all of which perform a similar oxygen transfer function. But there is no way to know for sure, since we have only one example of human evolution. Thus the reckoning used here, namely enumerating combinatorial possibilities and taking the reciprocal to obtain a probability figure, is unjustified and invalid.
In any event, it is clear that the impressive-sounding probability figure claimed by these writers is a vacuous arithmetic exercise, with no foundation in real empirical biology. For a detailed discussion of these issues, see Do probability arguments refute evolution?.
The post-hoc fallacy in finance
The field of finance is deeply afflicted by the post-hoc fallacy, because of “backtest overfitting,” namely the usage of historical market data to develop an investment model, strategy or fund, where many variations are tried on the same fixed dataset (note that this is unavoidably a post-hoc reckoning). Backtest overfitting has long plagued the field of finance and is now thought to be the leading reason why investments that look great when designed often disappoint when actually fielded to investors. Models, strategies and funds suffering from this type of statistical overfitting typically target the random patterns present in the limited in-sample test-set on which they are based, and thus often perform erratically when presented with new, truly out-of-sample data.
As an illustration, the authors of this AMS Notices article show that if only five years of daily stock market data are available as a backtest, then no more than 45 variations of a strategy should be tried on this data, or the resulting strategy will be overfit, in the specific sense that the strategy’s Sharpe Ratio (a standard measure of financial return) is likely to be 1.0 or greater just by chance, even though the true Sharpe Ratio may be zero or negative.
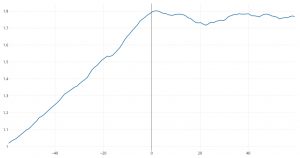
Comparison of index average excess return versus broad U.S. stock market: hypothetical growth of $1 over 60 months before and 60 months after inception of the index.
Data from Joel M. Dickson, Sachin Padmawar and Sarah Hammer, “Joined at the hip: ETF and index development,” July 2012, https://www.vanguardcanada.ca/documents/joined-at-the-hip.pdf.
Some commonly used techniques to compensate for backtest overfitting, if not used correctly, are themselves tantamount to overfitting. One example is the “hold-out method” — developing a model or investment fund based on a backtest of a certain date range, then checking the result with a different date range. However, those using the hold-out method may iteratively tune the parameters for their model until the score on the hold-out data, say measured by a Sharpe ratio, is impressively high. But these repeated tuning tests, using the same fixed hold-out dataset, are themselves tantamount to backtest overfitting (and thus subject to the post-hoc fallacy).
One dramatic visual example of backtest overfitting is shown in the graph at the right, which displays the mean excess return (compared to benchmarks) of newly minted exchange-traded index-linked funds, both in the months of design prior to submission to SEC for approval, and in the months after the fund was fielded. The “knee” in the graph at 0 shows unmistakably the difference between statistically overfit designs and actual field experience.
For additional details, see How backtest overfitting in finance leads to false discoveries, which appeared in the December 2021 issue of the British journal Significance. This Significance article is condensed from the following manuscript, which is freely available from SSRN: Finance is Not Excused: Why Finance Should Not Flout Basic Principles of Statistics.
Fermi’s paradox and the post-hoc fallacy
Most readers are likely familiar with Fermi’s paradox: There are at least 100 billion stars in the Milky Way, with many if not most now known to host planets. Once a species achieves a level of technology that is at least equal to ours, so that they have become a space-faring civilization, within a few million years (an eyeblink in cosmic time) they or their robotic spacecraft could fully explore the Milky Way. So why do we not see any evidence of their existence, or even of their exploratory spacecraft? For additional details, see this Math Scholar article.
Most “solutions” to Fermi’s paradox, including, sadly, some promulgated by prominent researchers who should know better, are easily defeated. For example, explanations such as “They are under strict orders not to communicate with a new civilization such as Earth,” or “They have lost interest in scientific research, exploration and expansion,” or “They have no interest in a primitive, backward society such as ours,” fall prey to a diversity argument: In any vast, diverse society (an essential prerequisite for advanced technology), there will be exceptions and nonconformists to any rule. Thus claims that “all extraterrestrials are like X” have little credibility, no matter what “X” is. It is deeply ironic that while most scientific researchers and others would strenuously reject stereotypes of religious, ethnic or national groups in human society, many seem willing to hypothesize sweeping, ironclad stereotypes for extraterrestrial societies.
Similarly, dramatic advances in human technology over the past decade, including new space exploration vehicles, new energy sources, state-of-the-art supercomputers, quantum computing, robotics and artificial intelligence, are severely undermining the long-standing assumption that space exploration is fundamentally too difficult.
One of the remaining explanations is that Earth is an exceedingly rare planet (possibly unique in the Milky Way), with a lengthy string of characteristics fostering a long-lived biological regime, which enabled the unlikely rise of intelligent life. John Gribbin, for example, writes “They are not here, because they do not exist. The reasons why we are here form a chain so improbable that the chance of any other technological civilization existing in the Milky Way Galaxy at the present time is vanishingly small.” [Gribbin2011, pg. 205]. Among other things, researchers note that:
- Very few (or possibly none) of the currently known exoplanets are likely to be truly habitable in all key factors (temperate, low radiation, water, dry land, position in galaxy, etc.). Exoplanets around brown dwarfs, for example, would be frequently bathed in sterilizing radiation. Thus Earth’s role as a cradle for life may well have been exceedingly rare.
- Even given a habitable environment, the origin of life on Earth is not well understood, in spite of decades of study, so it might well have been an exceedingly improbable event not repeated anywhere else in the Milky Way.
- Earth’s continual habitability over four billion years, facilitated in part by plate tectonics, geomagnetism and the ozone shield, might well be exceedingly rare.
- Even after life started, numerous key steps (photosynthesis, complex cells, complex structures) were required before advanced life could appear on Earth; each of these required many millions or even billions of years, suggesting that they may have been highly improbable.
- Even after the rise of complex creatures, the evolution of human-level intelligence may well be a vanishingly rare event; on Earth this happened only once among numerous continental “experiments” over the past 100 million years.
Note that any one of these five items may constitute a “great filter,” i.e. a virtually insuperable obstacle. Compounded together they suggest that the origin and rise of human-level technological life on Earth may well have been an exceedingly singular event in the cosmos, unlikely to be repeated anywhere else in the Milky Way if not beyond. Thus the “rare Earth” explanation of Fermi’s paradox is growing in credibility.
On the other hand, analyses in this arena are hobbled by the post-hoc probability fallacy: We only have one real data point, namely the rise of human technological civilization on a single planet, Earth, and so we have no way to rigorously assess the probability of our existence. It may be that the origin and rise of intelligent life is inevitable on any suitably hospitable planet, and we just need to keep trying to finally contact another similarly advanced species. Or it may be that the rise of a species with enough intelligence and technology to rigorously pose the question of its existence is merely a post-hoc selection effect — if we didn’t live on a hospitable planet that harbored the origin of life and was continuously habitable over billions of years, thus allowing the evolution of life that progressed to advanced technology, we would not be here to pose the question.
As Charles Lineweaver of the Australian National University has observed [Lineweaver2024b]:
Our existence on Earth can tell us little about the probability of the evolution of human-like intelligence in the Universe because even if this probability were infinitesimally small and there were only one planet with the kind of intelligence that can ask this question, we the question-askers would, of necessity, find ourselves on that planet.
For additional details, see Where are the extraterrestrials? Fermi’s paradox, diversity and the origin of life.
Fine-tuning of the universe and the post-hoc fallacy
The dilemma of whether our existence is “special” in some sense extends to the universe itself.
For several decades, researchers in the fields of physics and cosmology have puzzled over deeply perplexing indications, many of them highly mathematical in nature, that the universe seems inexplicably well-tuned to facilitate the evolution of atoms, complex molecular structures and sentient creatures. Some of these “cosmic coincidences” include the following (these and numerous others are presented and discussed in detail in a recent book by Lewis and Barnes):
- If the strong force were slightly stronger or slightly weaker (by just 1% in either direction), then there would be no carbon or any heavier elements anywhere in the universe, and thus no carbon-based life forms to contemplate this intriguing fact.
- Had the weak force been somewhat weaker, the amount of hydrogen in the universe would be greatly decreased, starving stars of fuel for nuclear energy and leaving the universe a cold and lifeless place.
- The neutron’s mass is very slightly more than the combined mass of a proton, an electron and a neutrino. But if its mass were lower by 1%, then all isolated protons would decay into neutrons, and no atoms other than hydrogen, helium, lithium and beryllium could form.
- There is a very slight anisotropy in the cosmic microwave background radiation (roughly one part in 100,000), which is just enough to permit the formation of stars and galaxies. If this anisotropy had been slightly larger or smaller, stable planetary systems could not have formed.
- The cosmological constant paradox derives from the fact that when one calculates, based on known principles of quantum mechanics, the “vacuum energy density” of the universe, one obtains the incredible result that empty space “weighs” 1093 grams per cubic centimeter, which is in error by 120 orders of magnitude from the observed level. Physicists thought that perhaps when the contributions of the other known forces are included, all terms will cancel out to exactly zero as a consequence of some heretofore unknown physical principle. But these hopes were shattered with the 1998 discovery that the expansion of the universe is accelerating, which implies that the cosmological constant must be slightly positive. Curiously, this observation is in accord with a prediction made by physicist Steven Weinberg in 1987, who argued from basic principles that the cosmological constant must be nonzero but within one part in roughly 10120 of zero, or else the universe either would have dispersed too fast for stars and galaxies to have formed, or would have recollapsed upon itself long ago. Numerous “solutions” have been proposed for the cosmological constant paradox (Lewis and Barnes mention eight — see pg. 163-164), but they all fail, rather miserably.
- A similar coincidence has come to light recently in the wake of the 2012 discovery of the Higgs boson at the Large Hadron Collider. Higgs was found to have a mass of 126 billion electron volts (i.e., 126 Gev). However, a calculation of interactions with other known particles yields a mass of some 1019 Gev. This means that the rest mass of the Higgs boson must be almost exactly the negative of this enormous number, so that when added to 1019 gives 126 Gev, as a result of massive and unexplained cancelation. This difficulty is known as the “hierarchy” problem.
- General relativity allows the space-time fabric of the universe to be open (extending forever, like an infinite saddle), closed (like the surface of a sphere), or flat. The latest measurements confirm that the universe is flat to within 1%. But looking back to the first few minutes of the universe at the big bang, this means that the universe must have been flat to within one part in 1015. The cosmic inflation theory was proposed by Alan Guth and others in the 1970s to explain this and some other phenomena, but recently even some of inflation’s most devoted proponents have acknowledged that the theory is in deep trouble and may have to be substantially revised.
- The overall entropy (disorder) of the universe is, in the words of Lewis and Barnes, “freakishly lower than life requires.” After all, life requires, at most, one galaxy of highly ordered matter to create chemistry and life on a single planet. Extrapolating back to the big bang only deepens this puzzle.
Numerous attempts at explanations have been proposed over the years to explain these difficulties. One of the more widely accepted hypotheses is the multiverse, combined with the anthropic principle. The theory of inflation, mentioned above, suggests that our universe is merely one pocket that separated from many others in the very early universe. Similarly, string theory suggests that our universe is merely one speck in an enormous landscape of possible universes, by one count 10500 in number, each corresponding to a different Calabi-Yau manifold.
Thus, the thinking goes, we should not be surprised that we find ourselves in a universe that has somehow beaten the one-in-10120 odds to be life-friendly (to pick just the cosmological constant paradox), because it had to happen somewhere, and, besides, if our universe were not life-friendly, then we would not be here to talk about it. In other words, these researchers propose that the multiverse (or the “cosmic landscape”) actually exists in some sense, but acknowledge that the vast majority of these universes are utterly sterile — either very short-lived or else completely devoid of atoms or other structures, much less sentient living organisms like us contemplating the meaning of their existence. We are just lucky.
But other researchers are very reluctant to adopt such reasoning. After all, we have no evidence of these other universes, and as yet we have no conceivable means of rigorously calculating the “probability” of any possible universe outcome, including ours (this is known as the “measure problem” of cosmology). As with Fermi’s paradox, by definition we have only one universe to observe and analyze, and thus, by the post-hoc probability fallacy, simple-minded attempts to reckon “probabilities” are doomed to failure.
For additional details, see Is the universe fine-tuned for intelligent life?.
Pinker on the post-hoc fallacy
A good introduction to the post-hoc probability fallacy for the general reader can be found in social scientist Steven Pinker’s new book Rationality: What It Is, Why It Seems Scarce, Why It Matters. Pinker likens the post-hoc fallacy to the following joke:
A man tries on a custom suit and says to the tailor, “I need this sleeve taken in.” The tailor says, “No, just bend your elbow like this. See, it pulls up the sleeve.” The customer says, “Well, OK, but when I bend my elbow, the collar goes up the back of my neck.” The tailor says, “So? Raise your head up and back. Perfect.” The man says, “But now the left shoulder is three inches lower than the right one!” The tailor says, “No problem. Bend at the waist and then it evens out.” The man leaves the store wearing the suit, his right elbow sticking out, his head craned back, his torso bent to the left, walking with a herky-jerky gait. A pair of pedestrians pass him by. The first says, “Did you see that poor disabled guy? My heart aches for him.” The second says, “Yeah, but his tailor is a genius — the suit fits him perfectly!”
