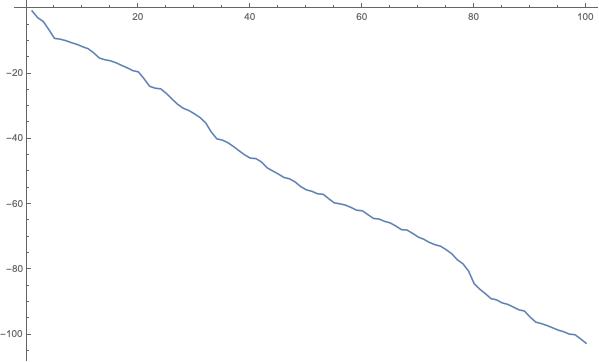
Log_10 of the error of a continued fraction approximation of Pi to k terms
Approximation of real numbers by rationals
The question of finding rational approximations to real numbers was first explored by the Greek scholar Diophantus of Alexandra (c. 201-285 BCE), and continues to fascinate mathematicians today, in a field known as Diophantine approximations.
It is easy to see that any real number can be approximated to any desired accuracy by simply taking the sequence of approximations given by the decimal digits out to some point, divided by the appropriate power of ten. For example, we can approximate $\pi$ to within one part in $10^{10}$ by simply writing $$\pi \approx \frac{31415926535}{10000000000}.$$
Researchers in the field have investigated more economical representations of this sort, in the sense of approximating a positive real number to a given tolerance by a rational whose denominator is small. One commonly used technique is the continued fraction algorithm, also known as the extended Euclidean algorithm. This operates by iteratively subtracting the greatest integer from the number, then taking the reciprocal, and then repeating, appropriately collecting the results along the way. For example, the first few approximations for $\pi$ produced in this manner are: $$3, \; 22/7, \; 333/106, \; 355/113, \; 103993/33102, \; 104348/33215, \; 208341/66317, \; \cdots.$$ The last approximation listed gives $\pi$ to approximately ten-digit accuracy, the same as for the digit expansion fraction above. See also the graph, which plots the logarithm base 10 of the error as a function of the number of steps taken in the algorithm applied to $\pi$.
Dirichlet’s approximation theorem
An important result in this arena is Dirichlet’s approximation theorem: For any real number $\alpha$ and integer $N \ge 1$, there exists a pair of integers $(p,q), 1 \leq q \leq N$, such that $|q \alpha – p| \leq 1/N$. An immediate corollary is that given any irrational $\alpha$, the inequality $$\left|\alpha – \frac{p}{q}\right| < \frac{1}{q^2}$$ is satisfied by infinitely many distinct integer pairs $(p,q)$. One might wonder whether the exponent 2 on the right-hand side can be increased, and still yield infinitely many distinct integer pairs. For irrational algebraic numbers, Roth’s theorem shows that the 2 cannot be improved: For every irrational algebraic $\alpha$ and $\epsilon > 0$, the inequality $$\left|\alpha – \frac{p}{q}\right| < \frac{1}{q^{2 + \epsilon}}$$ has only finitely many solutions in terms of relatively prime integers $(p,q)$. Conversely, if one can demonstrate, for a given irrational constant $\alpha$, that there are infinitely many distinct solution pairs $(p,q)$ satisfying the inequality with an exponent higher than 2, then, by Roth's theorem, $\alpha$ must be transcendental.
Khinchin’s theorem
Ever since Dirichlet first published his approximation theorem in 1840, researchers have explored generalizations, such as by considering different sequences of tolerances. In particular, let $\psi(q)$ be an arbitrary function from positive integers to nonnegative real numbers. Then given $\alpha \in [0,1]$, one can ask whether there are infinitely many pairs of integers $p,q$ such that $$\left|\alpha – \frac{p}{q}\right| \le \frac{\psi(q)}{q}.$$ As it turns out, the question is particularly difficult if $\psi(q)$ is somewhat irregular — for some $\psi$ and $\alpha$ there may be no solutions whatsoever. Nonetheless, one can show that under rather general conditions on $\psi$, this inequality will have infinitely many solutions for almost all $\alpha \in [0,1]$, in the measure theory sense.
One key result of this sort is Khinchin’s theorem: Suppose $\psi(q)$ is a function from the positive integers to nonnegative reals with the property that $q \psi(q)$ is decreasing, and let $\lambda$ denote Lebesque measure. Let $A$ denote the set of real $\alpha \in [0,1]$ for which the inequality $$\left|\alpha – \frac{p}{q}\right| \le \frac{\psi(q)}{q}$$ has infinitely many integer solution pairs $(p,q)$ with $0 \leq p \leq q$. Then (a): $\sum_q \psi(q) < \infty$ implies $\lambda(A) = 0$, and (b): $\sum_q \psi(q) = \infty$ implies $\lambda(A) = 1$.
The Duffin-Schaeffer conjecture
In 1941, Richard J. Duffin and Albert C. Schaeffer investigated Khinchin’s theorem to see if the condition $q \psi(q)$ decreasing could be relaxed. They found that it was more natural and promising to work with integer pairs $(p,q)$ that are relatively prime. Among other things, they were able to show, by applying the first Borel-Cantelli lemma, that if $\phi(q)$ is the Euler phi function, and $\psi(q)$ satisfies $$\sum_{q=1}^\infty \frac{\phi(q) \psi(q)}{q} < \infty,$$ then $\lambda(A) = 0$, where $A$ is as defined above except that the integer pair $(p,q)$ is relatively prime. This led them to conjecture, under the same assumptions, that if $$\sum_{q=1}^\infty \frac{\phi(q) \psi(q)}{q} = \infty,$$ then $\lambda(A) = 1$. This assertion (stated more precisely below) is now known as the Duffin-Schaeffer conjecture. While there have been numerous partial results, a full-fledged proof has eluded the mathematical research community for nearly 80 years.
Proof of the Duffin-Schaeffer conjecture
The surprising news is that the Duffin-Schaeffer has now been proven. In particular, in a new paper, Dimitris Koukoulopoulos of the University of Montreal and James Maynard of the University of Oxford have established the following:
Duffin-Schaeffer conjecture (now proven by Koukoulopoulos and Maynard): Let $\phi(q)$ denote Euler’s phi function, and suppose that $\psi(q)$ is a function from the positive integers to nonnegative reals with the property that $$\sum_{q=1}^\infty \frac{\phi(q) \psi(q)}{q} = \infty.$$ Let $\lambda$ denote Lebesque measure, and define $A$ as the set of real $\alpha \in [0,1]$ for which the inequality $$\left|\alpha – \frac{p}{q}\right| \le \frac{\psi(q)}{q}$$ has infinitely many distinct solutions with relatively prime integers $(p,q)$. Then $\lambda(A) = 1$.
Koukoulopoulos and Maynard adopted a novel approach for this problem: they recast the problem as a question about connections between points and lines in a graph. In particular, the authors created a graph out of the integer denominators, connecting the points representing denominators with a line if they share numerous prime factors. In this way, the graph’s structure encodes the overlap between irrational numbers approximated by each denominator. With this framework in place, Koukoulopoulos and Maynard were able to analyze the graph using known techniques from graph theory, which then yielded their result.
As Dimitris Koukoulopoulos explained, “The graph is a visual aid — it’s a very beautiful language in which to think about the problem.”
Reaction from the mathematical community
Reaction from the mathematical community has been swift and very complimentary. Jeffrey Vaaler of the University of Texas, Austin (who himself published some earlier results on the Duffin-Schaeffer conjecture) declared “It’s a beautiful piece of work.” He added, “They had what I’d say was a great deal of self-confidence, which was obviously justified, to go down the path they went down.”
For additional details, see this Quanta article by Kevin Hartnett, this Scientific American article by Leila Sloman, and, of course, the Koukoulopoulos-Maynard technical paper.