The standard model and the Lambda-CDM model
The standard model of physics, namely the framework of mathematical laws at the foundation of modern physics, has reigned supreme since the 1970, having been confirmed in countless exacting experimental tests. Perhaps its greatest success was the prediction of the Higgs boson, which was experimentally discovered in 2012, nearly 50 years after it was first predicted.
One application of the standard model, together with general relativity, is the Lambda Cold Dark Matter model (often abbreviated Lambda-CDM or Λ-CDM), which governs the evolution of the entire universe from the Big Bang to the present day. Among other things, this theory successfully explains:
- The cosmic microwave background radiation and its properties.
- The large-scale structure and distribution of galaxies.
- The present-day observed abundances of the light elements (hydrogen, deuterium, helium and lithium).
- The accelerating expansion of the universe, as observed in measurements of distant galaxies and supernovas.
Yet physicists have recognized for many years that neither the Lambda-CDM model nor the standard model itself can be the final answer. For example, quantum theory, the cornerstone of the standard model, is known to be mathematically incompatible with general relativity. Mathematical physicists are exploring string theory and loop quantum gravity as potential frameworks to resolve this incompatibility, but neither is remotely well-developed enough to qualify as a new “theory of everything.” In any event, there is only so far that mathematical analysis can go in the absence of solid experimental results. As Sabine Hossenfelder has emphasized, beautiful mathematics published in a vacuum of experimental data can lead physics astray.
The Hubble tension
There is one significant experimental anomaly that may point to a fundamental weakness in either the Lambda-CDM model or the standard model itself, namely a discrepancy in values of the Hubble constant based on different experimental approaches. The Hubble constant $H_0$ is a measure of the rate of expansion of the universe, and is directly connected to estimates of the age $A$ of the universe via the relation $A = 1 / H_0$. Units must be converted here, since the age of the universe is normally cited in billions of years, whereas the Hubble constant is usually given in kilometers per second per megaparsec (one megaparsec = $3.08567758128 \times 10^{19}$ km), and an adjustment factor is normally applied to this formula to be fully in conformance with the Big Bang model.
Researchers have long recognized this discrepancy, often termed the “Hubble tension,” but have presumed that sooner or later the various experimental approaches would finally converge. So far this has not happened; the latest results only deepen the discrepancy.
Latest experimental results
The various experimental methods that have been explored to produce values of $H_0$ can be categorized as “early universe” and “late universe” approaches. The early universe approaches are based the Lambda-CDM model together with careful analysis of cosmic microwave background (CMB) data. Here are the latest results from two groups employing this approach:
- One group has utilized the Planck satellite to obtain high-accuracy measurements of the CMB. Their latest results (2018) yielded $H_0 = 67.4 \pm 0.5$ km s-1 Mpc-1, which corresponds to $13.77$ billion years for the age of the universe.
- In July 2020, a team based at Princeton University announced a new result, based on the same Lambda-CDM model as the Planck team, but using the Atacama Cosmology Telescope (ACT) in Chile. Their result is $H_0 = 67.6 \pm 1.1$, which is within $0.3\%$ of the Planck team’s result.
The late universe approaches tend to employ more traditional astronomical techniques, typically based on observations of Cepheid variable stars and Type Ia supernovas, combined with parallax measurements as a calibration. Here are the latest results from teams using this approach:
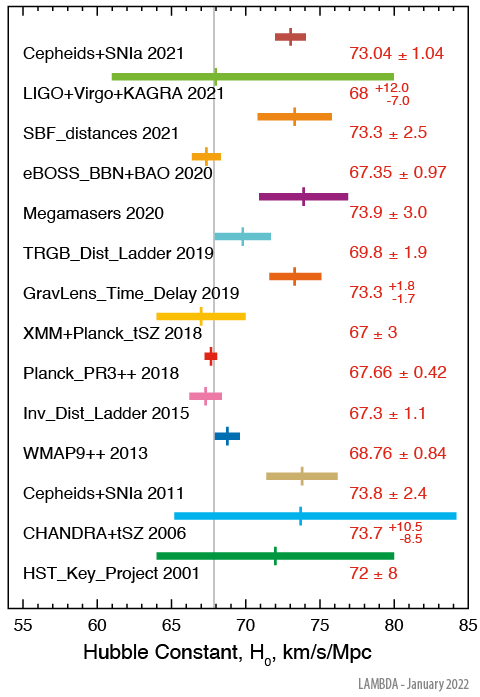
- In 2016, a team of astronomers led by Dan Scolnic of Duke University used the Wide Field Camera 3 (WFC3) of the Hubble Space Telescope to analyze a set of Cephid variable stars. They obtained the value $H_0 = 73.24 \pm 1.74$, corresponding to $12.67$ billion years for the age of the universe. In January 2022, the Duke group updated their results (see also this report). Using the Hubble Space Telescope as before, they analyzed Cepheid variable stars in the host galaxies of 42 Type Ia supernovas. The distances to the Cepheid variable stars were calibrated geometrically, using parallax measurements from the Gaia spacecraft, masers in the galaxy NGC4258, and detached eclipsing binary stars in the Large Magellanic Cloud. Their new result was $H_0 = 73.04 \pm 1.04$, not significantly different than before, but with tightened statistical error bounds that further highlights the inconsistency with values from the Planck and Princeton teams.
- In July 2019, a group headed by Wendy Freedman at the University of Chicago reported results from another late universe experimental approach, known as the “Tip of the Red Giant Branch” (TRGB). Their approach, which is analogous to but independent from the approach taken with Cepheid variable stars, is to analyze a surge in helium burning near the end of a red giant star’s lifetime. Using this scheme, they reported $H_0 = 69.8 \pm 1.7$, which is somewhat higher than the Planck and Princeton teams’ value, but not nearly enough to close the gap with the Duke University team. In February 2020, the Freedman group updated their TRGB study with additional consistency checks. Their updated result was $H_0 = 69.6 \pm 1.7$, a value close to the previous figure and still hopelessly inconsistent with the Duke and Princeton values.
- Another group, called $H_0$ Lenses in COSMOGRAIL’s Wellspring (HoLiCOW) project [yes, that really is the team’s acronym] announced results based on gravitational lensing of distant quasars by an intervening galaxy. When this happens, multiple time-delayed images of the galaxy appear at the edges of the intervening galaxy, when viewed by earth-bound astronomers. The HoLiCOW project’s latest result is $H_0 = 73.3 \pm 1.76$, very close to the Duke result.
- A group headed by researchers at the University of Oregon employed the baryonic Tully-Fisher relation (bTFR) as a distance estimator. Using 50 galaxies with accurate distances (from either Cepheid or TRGB measurements), they calibrated the bTFR on a large scale. After applying this calibrated bTFR model to 95 independent galaxies, they found $H_0 = 75.1 \pm 2.3$, even higher than the Duke team’s result.
- In January 2021, a team of astronomers used the infrared channel detector of the Hubble Space Telescope to estimate $H_0$ based on the surface brightness fluctuation (SBF) distances for 63 bright galaxies out to 100 megaparsecs. Their estimate: $H_0 = 73.3 \pm 0.7$, close to the Duke figure.
One interesting new approach utilized the Laser Interferometer Gravitational-Wave Observatory (LIGO) to analyze the amplitude of gravitational waves resulting from the merger binary neutron star systems. In November 2021, the KAGRA collaboration (a consortium of over 1600 researchers who work on LIGO) announced their estimate of the Hubble constant: $61 \leq H_0 \leq 80$, with $68$ as the most likely value. While these rather large error bounds do not help settle the current Hubble tension, researchers hope that future gravitational wave detections will provide tighter constraints.
A five-sigma discrepancy
Needless to say, researchers are perplexed by the latest reports: the Planck team reports $H_0 = 67.4 \pm 0.5$; the Princeton group reports $H_0 = 67.6 \pm 1.1$; the Chicago team reports $H_0 = 69.6 \pm 1.7$; the HoLiCOW team reports $H_0 = 73.3 \pm 1.76$; the SBF team reports $73.3 \pm 0.7$; the Duke team reports $H_0 = 73.04 \pm 1.04$; and the Oregon team reports $H_0 = 75.1 \pm 2.3$. Obviously these results cannot all simultaneously be correct. For example, the Duke figure ($73.04$) represents more than a five-sigma discrepancy from the Planck figure ($67.4$); i.e., there is only a one in 3.5 million chance that the discrepancy is merely due to a statistical fluke.
This graphic, taken from a NASA report, summarizes 14 different measurements and their standard error bars (references):
Are the mathematical models wrong?
While each of these teams is hard at work scrutinizing their methods and refining their results, researchers are increasingly considering the unsettling possibility that one or more of the underlying mathematical physics theories governing these phenomena (e.g., the Lambda-CDM model or even the standard model itself) are just plain wrong, at least on the length and time scales involved.
Yet researchers are loath to discard a theory that has explained so much so well (see summary in the second paragraph above). As Lloyd Knox, a cosmologist at the University of California, Davis, explains,
The Lambda-CDM model has been amazingly successful. … If there’s a major overhaul of the model, it’s hard to see how it wouldn’t look like a conspiracy. Somehow this ‘wrong’ model got it all right.
Various modifications to the Lambda-CDM model have been proposed, but while some of these changes partially alleviate the Hubble tension, others make it even worse. None of them is taken very seriously in the community at the present time.
Adam Riess, an astronomer at Johns Hopkins University in Baltimore, Maryland, is reassured that the Princeton ACT team’s result was so close to the Planck team’s result, and he hopes that additional experimental results will close the gap between the competing values. Nonetheless, he ventures, “My gut feeling is that there’s something interesting going on.”
For additional details and discussion, see this Scientific American article, this Quanta article, this Nature article and this Sky and Telescope article.
Caution
In spite of the temptation to jump to conclusions, considerable caution is in order before throwing out the Lambda-CDM framework, much less the standard model. After all, in most cases anomalies are eventually resolved, either as some defect of the experimental process or as a faulty application of the theory.
A good example of an experimental defect is the 2011 announcement by Italian scientists that neutrinos emitted at CERN (near Geneva, Switzerland) had arrived at the Gran Sasso Lab (in the Italian Alps) 60 nanoseconds sooner than if they had traveled at the speed of light. If upheld, this finding would have constituted a violation of Einstein’s theory of relativity. As it turns out, the experimental team subsequently discovered that the discrepancy was due to a loose fiber optic cable, which had introduced an error in the timing system.
A related example is the 2014 announcement, made with great public fanfare, that physicists had detected the signature of the inflation epoch of the Big Bang. Alas, the current consensus is that the experimental signature was due to dust in the Milky Way; the earlier claim of evidence for inflation is now officially dead.
A good example of misapplication of underlying theory is the solar neutrino anomaly, namely a discrepancy in the number of observed neutrinos emanating from the interior of the sun from what had been predicted (incorrectly, as it turned out) based on the standard model. In 1998, researchers discovered that the anomaly could be resolved if neutrinos have a very small but nonzero mass; then, by straightforward application of standard model, the flavor of neutrinos could change enroute from the sun to the earth, thus resolving the discrepancy. Takaaki Kajita and Arthur McDonald received the 2015 Nobel Prize in physics for this discovery.
In any event, sooner or later some experimental result may be found that fundamentally upsets currently accepted theoretical theories, either for the standard model or for a specific framework such as Lambda-CDM cosmology. Will the “Hubble tension” do the trick? Only time will tell.